Configuring an RDFS+ Inference Step
This topic provides guidance on configuring an RDFS+ Inference Step that uses RDFS+ and OWL rules to create new relationships based on the vocabularies in the existing data. The sections below describe each of the tabs and configuration options that are available when you create or edit an RDFS+ Inference Step.
Details
The Details tab includes options such as the name of the Step, the source data to act upon, and the Data Model to run the RDFS+ inference rules against.
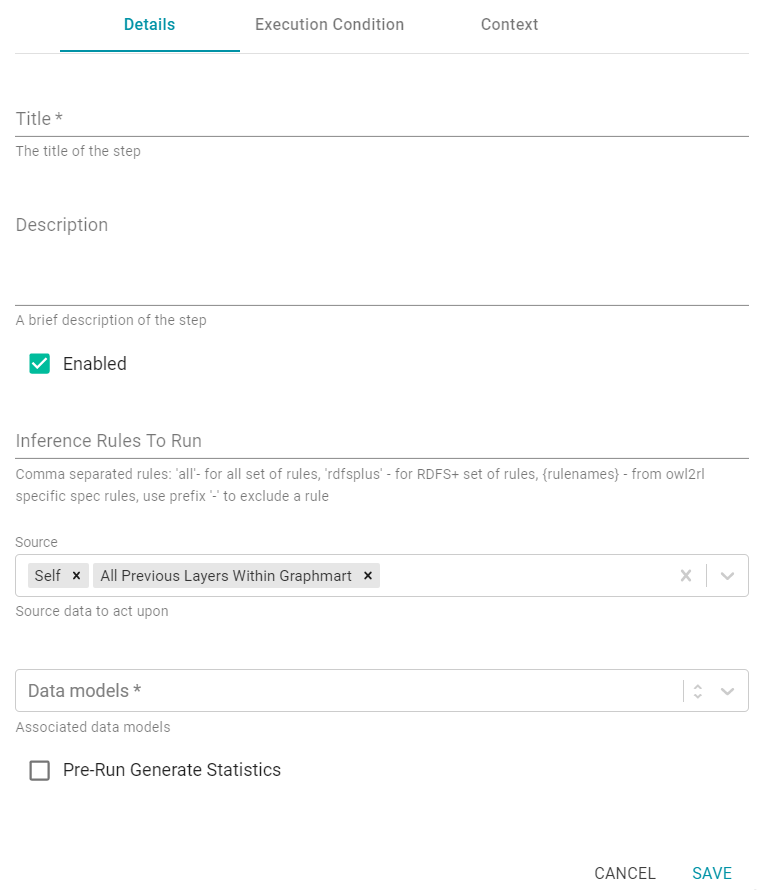
Title
The required name of the Step.
Description
And optional description of the Step.
Enabled
When creating a new Step, the Enabled option is selected by default, indicating that the Step is enabled and will run when the Data Layer is loaded or refreshed. If you want to disable the Step so that it is not processed, clear the Enabled checkbox.
Inference Rules to Run
By default the step runs all of the RDFS-plus inference rules and a subset of the OWL 2 RL rules (see Inference Rule Reference below for specifics). If you want to customize the step to include or exclude certain rules, specify any combination of the following options in the Inference Rules To Run field. Specify multiple options in a comma-separated list:
- all: Run all rules.
- rdfsplus: Run only the RDFS-plus rules.
- rule_names: List specific rules to run only those rules. See Inference Rule Reference.
- -rule_name: Specify a hyphen (-) in front of a rule name to exclude that rule. For example, -scm-svf2 excludes the scm-svf2 rule.
For example, the following value runs all of the inference rules except prp-fp and prp-ifp:
all,-prp-fp,-prp-ifp
Certain inference rules are coupled. Specifying either of the rules in the pair automatically runs the coupled rule. The list below describes the paired rules:
- scm-dom1 and scm-rng1
- scm-dom2 and scm-rng2
- prp-inv1 and prp-inv2
In addition, running scm-eqc1and cax-sco also runs cax-eqc1 and cax-eqc2. And running scm-eqp1 and prp-spo1 also runs prp-eqp1 and prp-eqp2.
Source
The Source is the source data that this Step should act upon. Steps can build upon the data generated by Steps in other Data Layers or can be self-contained, applying changes that relate only to the data defined in the Layer that contains this Step. You can select any number of the following options:
- Self: This option is selected by default and means that inferencing runs against only the data that is generated in the Layer this Step belongs to.
- All Previous Layers Within Graphmart: This option means that inferencing runs against the data that is generated by all of the Layers in the Graphmart that precede the Layer this step is in.
- Previous Layer Within Graphmart: This option means that inferencing runs against only the data that is generated by the one Layer that precedes the Layer this Step is in.
- Layer Name: The Source drop-down list also includes options for specific Layer names. You can choose a specific Layer to run inferencing against that Layer only.
Data Models
This required field specifies the Data Model or Models to associate with this Step. The list displays all of the Models for all of the Datasets in the Dataset catalog. By default, the field is set to Exclude System Data ( ). If you want to choose a system Model, click the toggle button on the right side of the field to change it to Include System Data (
). If you want to choose a system Model, click the toggle button on the right side of the field to change it to Include System Data ( ). The Data Models drop-down list will display the system Models in addition to the Dataset Models.
). The Data Models drop-down list will display the system Models in addition to the Dataset Models.
Pre-Run Generate Statistics
This option controls whether to initiate AnzoGraph's internal statistics gathering queries before running this Step. The statistics gathering helps ensure that the AnzoGraph query planner generates ideal query execution plans for queries that are run against the Graphmart.
Execution Condition
If you want this Step to be executed conditionally, based on the result of a specified Validation Condition, you can configure an Execution Condition on the Execution Condition tab that is available when creating or editing a Step. The image below shows the Execution Condition tab.
In order to set up an Execution Condition, the Graphmart needs to have at least one Validation Step that defines a Condition Variable. Condition Variables can be used across all Data Layers in the Graphmart. For guidance on configuring a Validation Step, see Configuring a Validation Step.

Enable Layer Based on Boolean Condition
This setting indicates whether to enable this Step only if the returned value from the Validation Condition is either true or false. You specify true or false in the Conditional Variable If Result field. If the Validation Condition fails, the Step is disabled.
Conditional Variable
This field specifies the variable that you want to base this Execution Condition on. The variable is the result of a Validation Step Query in the Graphmart.
Conditional Variable If Result
If you enabled the Enable Layer Based on Boolean Condition setting, select true or false from the drop-down list. The Step will be enabled only if the result of the Validation Step Query matches the value that you specified. If Enable Layer Based on Boolean Condition is disabled, leave this field blank.
Inference Rule Reference
This topic provides reference information for the RDFS-plus rules and the subset of OWL 2 RL rules that inference steps run.
RDFS+ Rules
The tables below define the RDFS-plus inference rules.
Semantics of Class Axioms
Because cax-eqc1 and cax-eqc2 (described in the table below) are implied rules that are coupled with scm-eqc1 and cax-sco, including cax-eqc1 or cax-eqc2 in the WITH RULES clause will result in an invalid inference rule name error. To run the cax-eqc1 and cax-eqc2 rules, specify scm-eqc1 and cax-sco (scm-eqc1,cax-sco) in the WITH RULES clause.
| Rule | Description | IF | THEN |
|---|---|---|---|
| cax-eqc1 | Two classes are synonymous. | T(?c1, owl:equivalentClass, ?c2)
T(?x, rdf:type, ?c1) |
T(?x, rdf:type, ?c2) |
| cax-eqc2 | Two classes are synonymous. | T(?c1, owl:equivalentClass, ?c2) T(?x, rdf:type, ?c2) |
T(?x, rdf:type, ?c1) |
| cax-sco | Members of a subclass are also members of the superclass. | T(?c1, rdfs:subClassOf, ?c2) T(?x, rdf:type, ?c1) |
T(?x, rdf:type, ?c2) |
Semantics of Axioms about Properties
Because prp-eqp1 and prp-eqp2 (described in the table below) are implied rules that are coupled with scm-eqp1 and prp-spo1, including prp-eqp1 or prp-eqp2 in the WITH RULES clause will result in an invalid inference rule name error. To run the prp-eqp1 and prp-eqp2 rules, specify scm-eqp1 and prp-spo1 (scm-eqp1,prp-spo1) in the WITH RULES clause.
| Rule | Description | IF | THEN |
|---|---|---|---|
| prp-dom | Infer the subject's type from the predicate's domain. | T(?p, rdfs:domain, ?c) T(?x, ?p, ?y) |
T(?x, rdf:type, ?c) |
| prp-eqp1 | Two properties are synonymous. | T(?p1, owl:equivalentProperty, ?p2) T(?x, ?p1, ?y) |
T(?x, ?p2, ?y) |
| prp-eqp2 | Two properties are synonymous. | T(?p1, owl:equivalentProperty, ?p2)
T(?x, ?p2, ?y) |
T(?x, ?p1, ?y) |
| prp-fp | If predicate p is a functional property, then a subject can be related to only one specific object by p. | T(?p, rdf:type, owl:FunctionalProperty) T(?x, ?p, ?y1) T(?x, ?p, ?y2) |
T(?y1, owl:sameAs, ?y2) |
| prp-ifp | If predicate p is an inverse functional property, then a specific object can be related to only one subject by p. | T(?p, rdf:type, owl:InverseFunctionalProperty) T(?x1, ?p, ?y) T(?x2, ?p, ?y) |
T(?x1, owl:sameAs, ?x2) |
| prp-inv1 | Two properties are the inverse of each other. | T(?p1, owl:inverseOf, ?p2)
T(?x, ?p1, ?y) |
T(?y, ?p2, ?x) |
| prp-inv2 | Two properties are the inverse of each other. | T(?p1, owl:inverseOf, ?p2) T(?x, ?p2, ?y) |
T(?y, ?p1, ?x) |
| prp-rng | Infer the object's type from the predicate's range. | T(?p, rdfs:range, ?c) T(?x, ?p, ?y) |
T(?y, rdf:type, ?c) |
| prp-spo1 | Relationships that are described by a subproperty also hold for the superproperty. | T(?p1, rdfs:subPropertyOf, ?p2) T(?x, ?p1, ?y) |
T(?x, ?p2, ?y) |
| prp-symp | The inverse is true for a property. | T(?p, rdf:type, owl:SymmetricProperty) T(?x, ?p, ?y) |
T(?y, ?p, ?x) |
| prp-trp | Chains of relationships collapse into a single relationship. | T(?p, rdf:type, owl:TransitiveProperty) T(?x, ?p, ?y) T(?y, ?p, ?z) |
T(?x, ?p, ?z) |
Semantics of Schema Vocabulary
| Rule | Description | IF | THEN |
|---|---|---|---|
| scm-cls | Every class is its own subclass and equivalent class, and it is a subclass of owl:Thing. | T(?c, rdf:type, owl:Class) | T(?c, rdfs:subClassOf, ?c) T(?c, owl:equivalentClass, ?c) T(?c, rdfs:subClassOf, owl:Thing) T(owl:Nothing, rdfs:subClassOf, ?c) |
| scm-dom1 | A property with domain c also has domain c's superclasses. | T(?p, rdfs:domain, ?c1) T(?c1, rdfs:subClassOf, ?c2) |
T(?p, rdfs:domain, ?c2) |
| scm-dom2 | A subproperty inherits the domains of the superproperties. | T(?p2, rdfs:domain, ?c) T(?p1, rdfs:subPropertyOf, ?p2) |
T(?p1, rdfs:domain, ?c) |
| scm-eqc1 | Equivalent classes are subclasses of each other. | T(?c1, owl:equivalentClass, ?c2) | T(?c1, rdfs:subClassOf, ?c2) T(?c2, rdfs:subClassOf, ?c1) |
| scm-eqc2 | If two classes are subclasses, they are also equivalent classes. | T(?c1, rdfs:subClassOf, ?c2) T(?c2, rdfs:subClassOf, ?c1) |
T(?c1, owl:equivalentClass, ?c2) |
| scm-eqp1 | Equivalent properties are subproperties of each other. | T(?p1, owl:equivalentProperty, ?p2) | T(?p1, rdfs:subPropertyOf, ?p2) T(?p2, rdfs:subPropertyOf, ?p1) |
| scm-eqp2 | If two properties are subproperties, they are also equivalent properties. | T(?p1, rdfs:subPropertyOf, ?p2) T(?p2, rdfs:subPropertyOf, ?p1) |
T(?p1, owl:equivalentProperty, ?p2) |
| scm-rng1 | A property with range c also has range c's superclasses. | T(?p, rdfs:range, ?c1) T(?c1, rdfs:subClassOf, ?c2) |
T(?p, rdfs:range, ?c2) |
| scm-rng2 | A subproperty inherits the ranges of its superproperties. | T(?p2, rdfs:range, ?c) T(?p1, rdfs:subPropertyOf, ?p2) |
T(?p1, rdfs:range, ?c) |
| scm-sco | owl:subClassOf relationships are transitive | T(?c1, rdfs:subClassOf, ?c2) T(?c2, rdfs:subClassOf, ?c3) |
T(?c1, rdfs:subClassOf, ?c3) |
| scm-spo | owl:subPropertyOf relationships are transitive. | T(?p1, rdfs:subPropertyOf, ?p2) T(?p2, rdfs:subPropertyOf, ?p3) |
T(?p1, rdfs:subPropertyOf, ?p3) |
The scm-dp and scm-op schema vocabulary rules are not run. Those rules add significant compute overhead but do not result in meaningful inference results.
OWL 2 RL Rules
The tables below define the subset of OWL 2 RL inference rules that inference steps run.
Semantics of Equality
| Rule | Description | IF | THEN |
|---|---|---|---|
| eq-rep-o | Describes the replacement property of the owl:sameAs axiom. | T(?o, owl:sameAs, ?o') T(?s, ?p, ?o) |
T(?s, ?p, ?o') |
| eq-rep-p | Describes the replacement property of the owl:sameAs axiom. | T(?p, owl:sameAs, ?p') T(?s, ?p, ?o) |
T(?s, ?p', ?o) |
| eq-rep-s | Describes the replacement property of the owl:sameAs axiom. | T(?s, owl:sameAs, ?s') T(?s, ?p, ?o) |
T(?s', ?p, ?o) |
| eq-sym | Describes the symmetric property of the owl:sameAs axiom. | T(?x, owl:sameAs, ?y) | T(?y, owl:sameAs, ?x) |
| eq-trans | Describes the transitive property of the owl:sameAs axiom. | T(?x, owl:sameAs, ?y) T(?y, owl:sameAs, ?z) |
T(?x, owl:sameAs, ?z) |
Semantics of Schema Vocabulary
| Rule | Description | IF | THEN |
|---|---|---|---|
| scm-svf1 | A property restriction c1 is a subclass of c2 if they are both someValuesFrom restrictions on the same property and c1's target class is a subclass of c2's target class. | T(?c1, owl:someValuesFrom, ?y1) T(?c1, owl:onProperty, ?p) T(?c2, owl:someValuesFrom, ?y2) T(?c2, owl:onProperty, ?p) T(?y1, rdfs:subClassOf, ?y2) |
T(?c1, rdfs:subClassOf, ?c2) |
| scm-svf2 | A property restriction c1 is a subclass of c2 if they are both someValuesFrom restrictions on the same class where c1's target property is a subproperty of c2's target property. | T(?c1, owl:someValuesFrom, ?y) T(?c1, owl:onProperty, ?p1) T(?c2, owl:someValuesFrom, ?y) T(?c2, owl:onProperty, ?p2) T(?p1, rdfs:subPropertyOf, ?p2) |
T(?c1, rdfs:subClassOf, ?c2) |
| scm-int | T(?c, owl:intersectionOf, ?x) LIST[?x, ?c1, ..., ?cn] |
T(?c, rdfs:subClassOf, ?c1) T(?c, rdfs:subClassOf, ?c2) ... T(?c, rdfs:subClassOf, ?cn) |
Semantics of Classes
| Rule | Description | IF | THEN |
|---|---|---|---|
| cls-svf1 | At least one object of a property is a member of the specified class. | T(?x, owl:someValuesFrom, ?y) T(?x, owl:onProperty, ?p) T(?u, ?p, ?v) T(?v, rdf:type, ?y) |
T(?u, rdf:type, ?x) |
| cls-int1 | An instance belongs to every one of the specified classes. | T(?c, owl:intersectionOf, ?x)
LIST[?x, ?c1, ..., ?cn] T(?y, rdf:type, ?c1) T(?y, rdf:type, ?c2) ... T(?y, rdf:type, ?cn) |
T(?y, rdf:type, ?c) |